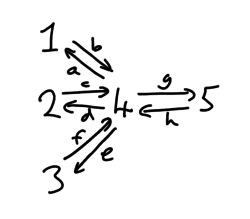Difference between revisions of "M(8,5,8)"
(Referencing) |
m |
||
| (One intermediate revision by the same user not shown) | |||
| Line 29: | Line 29: | ||
1 & 1 & 1 & 1 & 1 \\ | 1 & 1 & 1 & 1 & 1 \\ | ||
1 & 1 & 1 & 2 & 1 \\ | 1 & 1 & 1 & 2 & 1 \\ | ||
| − | \end{array}\right)</math><ref>Decomposition matrix taken from [http://www.math.rwth-aachen.de/~MOC/decomposition/], although it was first determined in [[References|[LM80]]] following partial results of Fong</ref> | + | \end{array}\right)</math><ref>Decomposition matrix taken from [http://www.math.rwth-aachen.de/~MOC/decomposition/], although it was first determined in [[References#L|[LM80]]] following partial results of Fong</ref> |
|O-morita-frob = 1 | |O-morita-frob = 1 | ||
| − | |Pic-O = | + | |Pic-O = <math>C_3</math><ref>See [[References#E|[EL18c]]]</ref> |
| + | |PIgroup = | ||
|source? = No | |source? = No | ||
|sourcereps = | |sourcereps = | ||
|k-derived-known? = Yes | |k-derived-known? = Yes | ||
| − | |k-derived = [[M(8,5,6)]], [[M(8,5,7)]]<ref>Derived equivalent by [[References|[GO97]]]</ref> | + | |k-derived = [[M(8,5,6)]], [[M(8,5,7)]]<ref>Derived equivalent by [[References#G|[GO97]]]</ref> |
| − | |O-derived-known? = Yes <ref>As noted in [[References|[CR13]]] the derived equivalences in [[References|[GO97]]] are [[Glossary#Splendid equivalence|splendid]] and so lift to <math>\mathcal{O}</math></ref> | + | |O-derived-known? = Yes <ref>As noted in [[References#C|[CR13]]] the derived equivalences in [[References#G|[GO97]]] are [[Glossary#Splendid equivalence|splendid]] and so lift to <math>\mathcal{O}</math></ref> |
|coveringblocks = Potentially [[M(8,5,5)]] | |coveringblocks = Potentially [[M(8,5,5)]] | ||
|coveredblocks = [[M(8,5,5)]] | |coveredblocks = [[M(8,5,5)]] | ||
| + | |pcoveringblocks = | ||
}} | }} | ||
| Line 51: | Line 53: | ||
== Other notatable representatives == | == Other notatable representatives == | ||
| − | <math>{\rm Aut (SL_2(8))} \cong {}^2G_2(3)</math>, and the blocks <math>B_0(\mathcal{O}({}^2G_2(3^{2m+1})))</math> are Morita equivalent for all <math>m</math>. This follows from Example 3.3 of [[References|[Ok97]]], where, as noted in 6.2.2 of [[References|[CR13]]] the Morita equivalence is [[Glossary#Splendid equivalence|splendid]] and so lifts to <math>\mathcal{O}</math> | + | <math>{\rm Aut (SL_2(8))} \cong {}^2G_2(3)</math>, and the blocks <math>B_0(\mathcal{O}({}^2G_2(3^{2m+1})))</math> are Morita equivalent for all <math>m</math>. This follows from Example 3.3 of [[References#O|[Ok97]]], where, as noted in 6.2.2 of [[References#C|[CR13]]] the Morita equivalence is [[Glossary#Splendid equivalence|splendid]] and so lifts to <math>\mathcal{O}</math> |
| − | By [[References|[Ea16]]] the principal block of each subgroup of <math>{\rm Aut}({}^2G_2(3^{2m+1}))</math> containing <math>{}^2G_2(3^{2m+1})</math> is in this Morita equivalence class. | + | By [[References#E|[Ea16]]] the principal block of each subgroup of <math>{\rm Aut}({}^2G_2(3^{2m+1}))</math> containing <math>{}^2G_2(3^{2m+1})</math> is in this Morita equivalence class. |
== Projective indecomposable modules == | == Projective indecomposable modules == | ||
| − | Labelling the simple <math>B</math>-modules by <math>1,2,3,4,5</math>, the projective indecomposable modules have Loewy structure as follows<ref>The structure of the projective indecomposable modules was first given in [[References|[LM80]]], although with a mistake corrected in [[References|[GO97]]]</ref>: | + | Labelling the simple <math>B</math>-modules by <math>1,2,3,4,5</math>, the projective indecomposable modules have Loewy structure as follows<ref>The structure of the projective indecomposable modules was first given in [[References#L|[LM80]]], although with a mistake corrected in [[References#G|[GO97]]]</ref>: |
<math>\begin{array}{ccccc} | <math>\begin{array}{ccccc} | ||
Latest revision as of 14:22, 12 April 2019
| Representative: | [math]B_0(k(\rm Aut (SL_2(8))))[/math] |
|---|---|
| Defect groups: | [math]C_2 \times C_2 \times C_2[/math] |
| Inertial quotients: | [math]C_7:C_3[/math] |
| [math]k(B)=[/math] | 8 |
| [math]l(B)=[/math] | 5 |
| [math]{\rm mf}_k(B)=[/math] | 1 |
| [math]{\rm Pic}_k(B)=[/math] | |
| Cartan matrix: | [math]\left( \begin{array}{ccccccc} 4 & 2 & 2 & 4 & 2 \\ 2 & 4 & 2 & 4 & 2 \\ 2 & 2 & 4 & 4 & 2 \\ 4 & 4 & 4 & 8 & 3 \\ 2 & 2 & 2 & 3 & 2 \\ \end{array} \right)[/math] |
| Defect group Morita invariant? | Yes |
| Inertial quotient Morita invariant? | Yes |
| [math]\mathcal{O}[/math]-Morita classes known? | Yes |
| [math]\mathcal{O}[/math]-Morita classes: | [math]B_0(\mathcal{O}(\rm Aut (SL_2(8))))[/math] |
| Decomposition matrices: | [math]\left( \begin{array}{ccccc} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & 0 \\ 0 & 0 & 1 & 1 & 0 \\ 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 2 & 1 \\ \end{array}\right)[/math][1] |
| [math]{\rm mf}_\mathcal{O}(B)=[/math] | 1 |
| [math]{\rm Pic}_{\mathcal{O}}(B)=[/math] | [math]C_3[/math][2] |
| [math]PI(B)=[/math] | |
| Source algebras known? | No |
| Source algebra reps: | |
| [math]k[/math]-derived equiv. classes known? | Yes |
| [math]k[/math]-derived equivalent to: | M(8,5,6), M(8,5,7)[3] |
| [math]\mathcal{O}[/math]-derived equiv. classes known? | Yes [4] |
| [math]p'[/math]-index covering blocks: | Potentially M(8,5,5) |
| [math]p'[/math]-index covered blocks: | M(8,5,5) |
| Index [math]p[/math] covering blocks: |
The principal 2-blocks of all Ree groups [math]{}^2G_2(3^{2m+1})[/math] belong to this Morita equivalence class.
Contents
Basic algebra
Quiver: a:<4,1>, b:<1,4>, c:<2,4>, d:<4,2>, e:<4,3>, f:<3,4>, g:<4,5>, h:<5,4>[5]
Relations w.r.t. [math]k[/math]:
Other notatable representatives
[math]{\rm Aut (SL_2(8))} \cong {}^2G_2(3)[/math], and the blocks [math]B_0(\mathcal{O}({}^2G_2(3^{2m+1})))[/math] are Morita equivalent for all [math]m[/math]. This follows from Example 3.3 of [Ok97], where, as noted in 6.2.2 of [CR13] the Morita equivalence is splendid and so lifts to [math]\mathcal{O}[/math]
By [Ea16] the principal block of each subgroup of [math]{\rm Aut}({}^2G_2(3^{2m+1}))[/math] containing [math]{}^2G_2(3^{2m+1})[/math] is in this Morita equivalence class.
Projective indecomposable modules
Labelling the simple [math]B[/math]-modules by [math]1,2,3,4,5[/math], the projective indecomposable modules have Loewy structure as follows[6]:
[math]\begin{array}{ccccc} \begin{array}{c} 1 \\ 4 \\ 1 \ 2 \ 3 \ 5 \\ 4 \ 4 \\ 1 \ 2 \ 3 \ 5 \\ 4 \\ 1 \\ \end{array}, & \begin{array}{c} 2 \\ 4 \\ 1 \ 2 \ 3 \ 5 \\ 4 \ 4 \\ 1 \ 2 \ 3 \ 5 \\ 4 \\ 2 \\ \end{array}, & \begin{array}{c} 3 \\ 4 \\ 1 \ 2 \ 3 \ 5 \\ 4 \ 4 \\ 1 \ 2 \ 3 \ 5 \\ 4 \\ 3 \\ \end{array}, & \begin{array}{c} 4 \\ 1 \ 2 \ 3 \ 5 \\ 4 \ 4 \ 4 \\ 1 \ 1 \ 2 \ 2 \ 3 \ 3 \ 5 \\ 4 \ 4 \ 4 \\ 1 \ 2 \ 3 \ 5 \\ 4 \\ \end{array}, & \begin{array}{c} 5 \\ 4 \\ 1 \ 2 \ 3 \\ 4 \\ 1 \ 2 \ 3 \\ 4 \\ 5 \\ \end{array} \end{array} [/math]
Irreducible characters
All irreducible characters have height zero.
Notes
- ↑ Decomposition matrix taken from [1], although it was first determined in [LM80] following partial results of Fong
- ↑ See [EL18c]
- ↑ Derived equivalent by [GO97]
- ↑ As noted in [CR13] the derived equivalences in [GO97] are splendid and so lift to [math]\mathcal{O}[/math]
- ↑ Computed using MAGMA
- ↑ The structure of the projective indecomposable modules was first given in [LM80], although with a mistake corrected in [GO97]