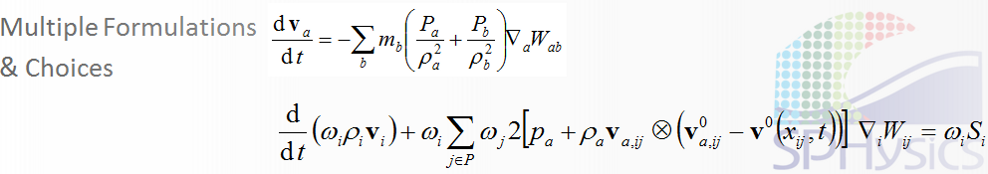





SWE-SPHysics
From SPHYSICS
(Difference between revisions)
| Line 3: | Line 3: | ||
|The two-dimensional shallow-water equations (SWEs) are widely used to approximate flows for a wide range of rapidly (and slowly) varying free-surface flows, such as dam breaks, river flooding, and tidal flows including storm surge and wave overtopping causing inundation in estuaries and coastal regions. Grid-based solvers are now widely available. Although accurate and robust wetting and drying routines have been developed, grid-based solvers are limited in simulating multi-phase effects, most importantly flows with rapid distortion in flood modelling. | |The two-dimensional shallow-water equations (SWEs) are widely used to approximate flows for a wide range of rapidly (and slowly) varying free-surface flows, such as dam breaks, river flooding, and tidal flows including storm surge and wave overtopping causing inundation in estuaries and coastal regions. Grid-based solvers are now widely available. Although accurate and robust wetting and drying routines have been developed, grid-based solvers are limited in simulating multi-phase effects, most importantly flows with rapid distortion in flood modelling. | ||
|- | |- | ||
| − | |Here, the SPHysics numerical scheme, originally developed to solve Navier-Stokes Equations has been extended to shallow water equations. | + | |Here, the SPHysics numerical scheme, originally developed to solve Navier-Stokes Equations has been extended to shallow water equations. |
| + | <br/> | ||
| + | |- | ||
| + | |'''Developers:''' Dr Renato Vacondio, Dr Benedict Rogers, Prof. Peter Stansby, Prof. Paolo Mignosa | ||
| + | <br/> | ||
|- | |- | ||
| | | | ||
| Line 25: | Line 29: | ||
|width="45%"| | |width="45%"| | ||
==1-D Test Cases== | ==1-D Test Cases== | ||
| − | * 1-D Wet-bed Dam break | + | * 1-D Wet-bed Dam break |
| − | * 1-D Dry-bed Dam break | + | * 1-D Dry-bed Dam break |
* 1-D Flow over hump with Inflow-Outflow | * 1-D Flow over hump with Inflow-Outflow | ||
|width="35%"| | |width="35%"| | ||
| Line 46: | Line 50: | ||
|- | |- | ||
|} | |} | ||
| + | ''Released March 2013'' | ||
| + | |||
| + | |||
| + | '''[[SWE-SPHYSICS_1D_Download_v1.0 | SWE-SPHYSICS_1D_v1.0 ]]''' March 2013 | ||
| + | |||
| + | '''[[SWE-SPHYSICS_2D_Download_v1.0 | SWE-SPHYSICS_2D_v1.0 ]]''' March 2013 | ||
| + | |||
| + | |||
| + | ''' Documentation of the shallow water equation (SWE) code: ''' | ||
| + | |||
| + | '''[[Media:SWE-SPHysics v1.0.00.pdf | SWE-SPHysics v1.0.00.pdf]]''' March 2013 | ||
How to reference: '''[[SPHYSICS Reference| How to reference SWE-SPHysics]]'''. | How to reference: '''[[SPHYSICS Reference| How to reference SWE-SPHysics]]'''. | ||
Revision as of 20:30, 16 February 2014
| The two-dimensional shallow-water equations (SWEs) are widely used to approximate flows for a wide range of rapidly (and slowly) varying free-surface flows, such as dam breaks, river flooding, and tidal flows including storm surge and wave overtopping causing inundation in estuaries and coastal regions. Grid-based solvers are now widely available. Although accurate and robust wetting and drying routines have been developed, grid-based solvers are limited in simulating multi-phase effects, most importantly flows with rapid distortion in flood modelling. |
| Here, the SPHysics numerical scheme, originally developed to solve Navier-Stokes Equations has been extended to shallow water equations.
|
| Developers: Dr Renato Vacondio, Dr Benedict Rogers, Prof. Peter Stansby, Prof. Paolo Mignosa
|
|
Key code features:
|
1-D Test Cases
|
2-D Test Cases
|
Released March 2013
SWE-SPHYSICS_1D_v1.0 March 2013
SWE-SPHYSICS_2D_v1.0 March 2013
Documentation of the shallow water equation (SWE) code:
SWE-SPHysics v1.0.00.pdf March 2013
How to reference: How to reference SWE-SPHysics.