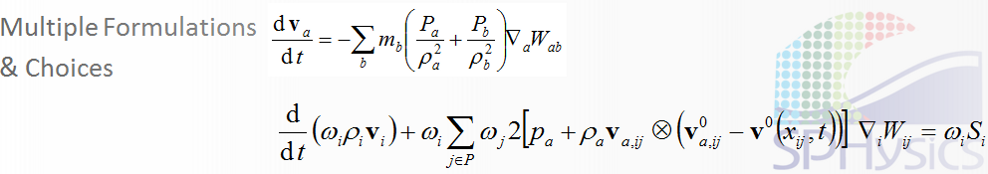





SWE-SPHysics
From SPHYSICS
(Difference between revisions)
| (2 intermediate revisions by one user not shown) | |||
| Line 1: | Line 1: | ||
| − | The two-dimensional shallow-water equations (SWEs) are widely used to approximate flows for a wide range of rapidly (and slowly) varying free-surface flows, such as dam breaks, river flooding, and tidal flows including storm surge and wave overtopping causing inundation in estuaries and coastal regions. Grid-based solvers are now widely available. Although accurate and robust wetting and drying routines have been developed, grid-based solvers are limited in simulating multi-phase effects, most importantly flows with rapid distortion in flood modelling | + | {| width="85%" |
| − | + | |- | |
| − | Here, the SPHysics numerical scheme, originally developed to solve Navier-Stokes Equations has been extended to shallow water equations. | + | |The two-dimensional shallow-water equations (SWEs) are widely used to approximate flows for a wide range of rapidly (and slowly) varying free-surface flows, such as dam breaks, river flooding, and tidal flows including storm surge and wave overtopping causing inundation in estuaries and coastal regions. Grid-based solvers are now widely available. Although accurate and robust wetting and drying routines have been developed, grid-based solvers are limited in simulating multi-phase effects, most importantly flows with rapid distortion in flood modelling. |
| + | |- | ||
| + | |Here, the SPHysics numerical scheme, originally developed to solve Navier-Stokes Equations has been extended to shallow water equations. | ||
| + | <br/> | ||
| + | |- | ||
| + | |'''Developers:''' Dr Renato Vacondio, Dr Benedict Rogers, Prof. Peter Stansby, Prof. Paolo Mignosa | ||
| + | <br/> | ||
| + | |- | ||
| + | | | ||
Key code features: | Key code features: | ||
| Line 12: | Line 20: | ||
* Bed Topography Representation | * Bed Topography Representation | ||
* Viscosity & Stabilisation terms | * Viscosity & Stabilisation terms | ||
| + | |||
The code comes with the following test cases: | The code comes with the following test cases: | ||
| + | |} | ||
{|cellpadding="10" width="85%" | {|cellpadding="10" width="85%" | ||
| Line 19: | Line 29: | ||
|width="45%"| | |width="45%"| | ||
==1-D Test Cases== | ==1-D Test Cases== | ||
| − | * 1-D Wet-bed Dam break | + | * 1-D Wet-bed Dam break |
| − | * 1-D Dry-bed Dam break | + | * 1-D Dry-bed Dam break |
* 1-D Flow over hump with Inflow-Outflow | * 1-D Flow over hump with Inflow-Outflow | ||
|width="35%"| | |width="35%"| | ||
| Line 40: | Line 50: | ||
|- | |- | ||
|} | |} | ||
| + | ''Released March 2013'' | ||
| + | |||
| + | |||
| + | '''[[SWE-SPHYSICS_1D_Download_v1.0 | SWE-SPHYSICS_1D_v1.0 ]]''' March 2013 | ||
| + | |||
| + | '''[[SWE-SPHYSICS_2D_Download_v1.0 | SWE-SPHYSICS_2D_v1.0 ]]''' March 2013 | ||
| + | |||
| + | |||
| + | ''' Documentation of the shallow water equation (SWE) code: ''' | ||
| + | |||
| + | '''[[Media:SWE-SPHysics v1.0.00.pdf | SWE-SPHysics v1.0.00.pdf]]''' March 2013 | ||
How to reference: '''[[SPHYSICS Reference| How to reference SWE-SPHysics]]'''. | How to reference: '''[[SPHYSICS Reference| How to reference SWE-SPHysics]]'''. | ||
| + | |||
| + | === Publications === | ||
| + | #'''Vacondio R, Rogers B D, Stansby P K, Mignosa P.''' "A correction for balancing discontinuous bed slopes in two-dimensional smoothed particle hydrodynamics shallow water modeling". ''International Journal for Numerical Methods in Fluids''. Vol. 71. Issue 7. pp 850-872. March. '''[http://dx.doi.org/10.1002/fld.3687 DOI: 10.1002/fld.3687], 2013'''. | ||
| + | #'''Vacondio R, Rogers B D, Stansby P K, Mignosa P.''' "Shallow water SPH for flooding with dynamic particle coalescing and splitting". ''Advances in Water Resources''. Vol. 58. pp 10-23. August. '''[http://dx.doi.org/10.1016/j.advwatres.2013.04.007 DOI: 10.1016/j.advwatres.2013.04.007], 2013'''. | ||
| + | #'''Vacondio R., Rogers B.D., Stansby P.K.'''. In Press. "Accurate particle splitting for SPH in shallow water with shock capturing". ''International Journal for Numerical Methods in Fluids'', Vol. 69. Issue 8. pp 1377-1410. '''[http://dx.doi.org/10.1002/fld.2646 DOI: 10.1002/fld.2646], 2012'''. | ||
| + | #'''Vacondio R., Rogers B.D., Stansby P.K'''. "Smoothed Particle Hydrodynamics: approximate zero-consistent 2-D boundary conditions and still shallow water tests". ''International Journal for Numerical Methods in Fluids'', Vol. 69. Issue 1. pp 226-253. '''[http://dx.doi.org/10.1002/fld.2559 DOI: 10.1002/fld.2559], 2011'''. | ||
Latest revision as of 23:03, 16 February 2014
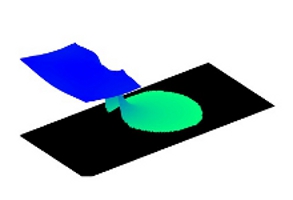
| The two-dimensional shallow-water equations (SWEs) are widely used to approximate flows for a wide range of rapidly (and slowly) varying free-surface flows, such as dam breaks, river flooding, and tidal flows including storm surge and wave overtopping causing inundation in estuaries and coastal regions. Grid-based solvers are now widely available. Although accurate and robust wetting and drying routines have been developed, grid-based solvers are limited in simulating multi-phase effects, most importantly flows with rapid distortion in flood modelling. |
| Here, the SPHysics numerical scheme, originally developed to solve Navier-Stokes Equations has been extended to shallow water equations.
|
| Developers: Dr Renato Vacondio, Dr Benedict Rogers, Prof. Peter Stansby, Prof. Paolo Mignosa
|
|
Key code features:
|
1-D Test Cases
|
2-D Test Cases
|
Released March 2013
SWE-SPHYSICS_1D_v1.0 March 2013
SWE-SPHYSICS_2D_v1.0 March 2013
Documentation of the shallow water equation (SWE) code:
SWE-SPHysics v1.0.00.pdf March 2013
How to reference: How to reference SWE-SPHysics.
Publications
- Vacondio R, Rogers B D, Stansby P K, Mignosa P. "A correction for balancing discontinuous bed slopes in two-dimensional smoothed particle hydrodynamics shallow water modeling". International Journal for Numerical Methods in Fluids. Vol. 71. Issue 7. pp 850-872. March. DOI: 10.1002/fld.3687, 2013.
- Vacondio R, Rogers B D, Stansby P K, Mignosa P. "Shallow water SPH for flooding with dynamic particle coalescing and splitting". Advances in Water Resources. Vol. 58. pp 10-23. August. DOI: 10.1016/j.advwatres.2013.04.007, 2013.
- Vacondio R., Rogers B.D., Stansby P.K.. In Press. "Accurate particle splitting for SPH in shallow water with shock capturing". International Journal for Numerical Methods in Fluids, Vol. 69. Issue 8. pp 1377-1410. DOI: 10.1002/fld.2646, 2012.
- Vacondio R., Rogers B.D., Stansby P.K. "Smoothed Particle Hydrodynamics: approximate zero-consistent 2-D boundary conditions and still shallow water tests". International Journal for Numerical Methods in Fluids, Vol. 69. Issue 1. pp 226-253. DOI: 10.1002/fld.2559, 2011.