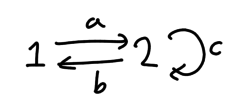M(27,1,3)
Revision as of 17:54, 6 September 2018 by Charles Eaton (talk | contribs) (Created page with "{{blockbox |title = M(27,1,3) - <math>B_0(kPSL_2(53))</math> |image = M(5,1,3)quiver.png |representative = <math>B_0(kPSL_2(53))</math> |defect = <math>C_{27}</math>...")
M(27,1,3) - [math]B_0(kPSL_2(53))[/math]
| Representative: | [math]B_0(kPSL_2(53))[/math] |
|---|---|
| Defect groups: | [math]C_{27}[/math] |
| Inertial quotients: | [math]C_2[/math] |
| [math]k(B)=[/math] | 15 |
| [math]l(B)=[/math] | 2 |
| [math]{\rm mf}_k(B)=[/math] | 1 |
| [math]{\rm Pic}_k(B)=[/math] | |
| Cartan matrix: | [math]\left( \begin{array}{cc} 2 & 1 \\ 1 & 14 \\ \end{array} \right)[/math] |
| Defect group Morita invariant? | Yes |
| Inertial quotient Morita invariant? | Yes |
| [math]\mathcal{O}[/math]-Morita classes known? | Yes |
| [math]\mathcal{O}[/math]-Morita classes: | [math]B_0(\mathcal{O} PSL_2(53))[/math] |
| Decomposition matrices: | [math]\left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \\ 0 & 1 \\ \vdots & \vdots \\ 0 & 1 \\ 1 & 1 \\ \end{array}\right)[/math] |
| [math]{\rm mf}_\mathcal{O}(B)=[/math] | 1 |
| [math]{\rm Pic}_{\mathcal{O}}(B)=[/math] | |
| [math]PI(B)=[/math] | {{{PIgroup}}} |
| Source algebras known? | Yes |
| Source algebra reps: | |
| [math]k[/math]-derived equiv. classes known? | Yes |
| [math]k[/math]-derived equivalent to: | M(27,1,2) |
| [math]\mathcal{O}[/math]-derived equiv. classes known? | Yes |
| [math]p'[/math]-index covering blocks: | {{{coveringblocks}}} |
| [math]p'[/math]-index covered blocks: | {{{coveredblocks}}} |
| Index [math]p[/math] covering blocks: | {{{pcoveringblocks}}} |
Contents
Basic algebra
Quiver: a:<1,2>, b:<2,1>, c:<2,2>
Relations w.r.t. [math]k[/math]: ac=cb=ba-c^{13}=0
Other notatable representatives
Covering blocks and covered blocks
Projective indecomposable modules
Labelling the simple [math]B[/math]-modules by [math]S_1, S_2[/math], the projective indecomposable modules have Loewy structure as follows:
[math]\begin{array}{cc} \begin{array}{c} S_1 \\ S_2 \\ S_1 \\ \end{array}, & \begin{array}{ccc} & S_2 & \\ S_1 & & \begin{array}{c} S_2 \\ S_2 \\ \vdots \\ S_2 \\ \end{array} \\ & S_2 & \\ \end{array} \end{array} [/math]
Irreducible characters
All irreducible characters have height zero.